REAL NUMBERS SYSTEM...
The Real Number System
All numbers that will be mentioned in this lesson belong to the set of the Real numbers. The set of the real numbers is denoted by the symbol . There are five subsets within the set of real numbers. Let’s go over each one of them.
Five (5) Subsets of Real Numbers
1) The Set of Natural or Counting Numbers
The set of the natural numbers (also known as counting numbers) contains the elements,

The ellipsis “…” signifies that the numbers go on forever in that pattern.
2) The Set of Whole Numbers
The set of whole numbers includes all the elements of the natural numbers plus the number zero (0).

The slight addition of the element zero to the set of natural numbers generates the new set of whole numbers. Simple as that!
3) The Set of Integers
The set of integers includes all the elements of the set of whole numbers and the opposites or “negatives” of all the elements of the set of counting numbers.

4) The Set of Rational Numbers
The set of rational numbers includes all numbers that can be written as a fraction or as a ratio of integers. However, the denominator cannot be equal to zero.

A rational number may also appear in the form of a decimal. If a decimal number is repeating or terminating, it can be written as a fraction, therefore, it must be a rational number.
Examples of terminating decimals:
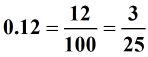
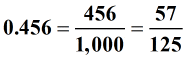
Examples of repeating decimals:
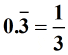
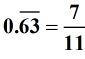

5) The Set of Irrational Numbers
The set of irrational numbers can be described in many ways. These are the common ones.
a) Irrational numbers are numbers that cannot be written as a ratio of two integers. This description is exactly the opposite that of the rational numbers.
b) Irrational numbers are the leftover numbers after all rational numbers are removed from the set of the real numbers. You may think of it as,
irrational numbers = real numbers “minus” rational numbers
c) Irrational numbers if written in decimal forms don’t terminate and don’t repeat.
There’s really no standard symbol to represent the set of irrational numbers. But you may encounter the one below.

Examples:
a) Pi
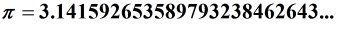
b) Euler’s number
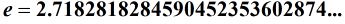
c) The square root of 2
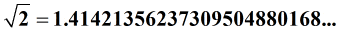

.jpg)
Comments
Post a Comment